Technical Notes > The HFSS Solution Process > Frequency Sweeps
Interpolating Frequency Sweeps
An Interpolating sweep estimates a solution for an entire frequency range. HFSS chooses the frequency points at which to solve the field solution so that the entire interpolated solution lies within a specified error tolerance. The sweep is complete when the solution meets the error tolerance criterion or generates the maximum number of solutions. To view more information about the solution, increase the number of steps and perform the sweep again.
The field solution for each point is deleted so that a new field solution can be generated for the next point. The full-field solution is only saved for the final frequency point computed. The S-parameters are saved for every solved frequency point.
Choose an Interpolating sweep if the frequency range is wide and the frequency response is smooth with the exception of a few resonances, or if the memory requirements of a Fast sweep exceed your resources. An Interpolating sweep’s time requirement may be much less than a Discrete sweep’s because a solution for the entire frequency range is interpolated based on solutions for a minimal number of frequency points. The maximum time required for an Interpolating sweep is the time required for a single frequency solution multiplied by the maximum number of solutions.
Be aware that HFSS uses the finite element mesh refined during an adaptive solution at the solution frequency or, if you did not request an adaptive solution, the initial mesh generated for the problem. It uses this mesh without further refinement.
The procedure for an Interpolating sweep is shown below, where n frequencies determined by the system are included in the sweep.
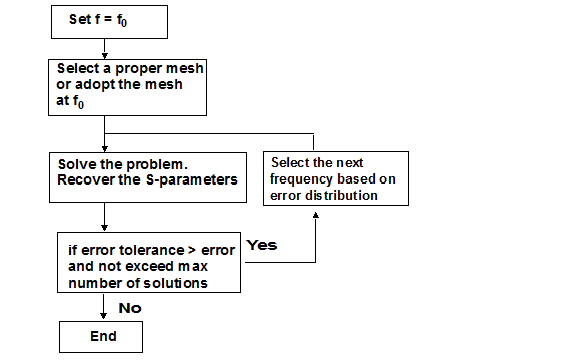
-

国内最全面的HFSS培训课程,包含7套视频教程和2本教材,资深专家讲解,视频操作演示,结合最新工程案例,让HFSS学习不再难...【详细介绍】





