|
 Ansoft Designer / Ansys Designer 在线帮助文档: Ansoft Designer / Ansys Designer 在线帮助文档:
System Simulator >
System Component Models >
Coders/Decoders >
Reed-Solomon Coder (RSCOD)
Reed-Solomon Coder (RSCOD)

Limits
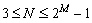
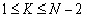
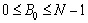
Notes
This model is used to perform Reed-Solomon (RS) encoding.
RS codes are a non-binary subclass of the BCH block codes. The
code format is RS(n,k) defined on Galois Field (2m).
The error correcting capability of the RS(n,k) code is defined
by t = (n-k)/2, which means this code can correct up to t
= (n-k)/2 errors.
The RS coder adds a sequence of 2t parity code symbols to each
k input data symbols to form a codeword with n = 2m-1
symbols. However, RS(n,k) can be shorten into RS(n-j, k-j)
by simply forcing j leading input data symbols to be zeros, and
then deleting these zero symbols from a systematic codeword.
For example, the digital satellite communications Reed-Solomon (RS)
coder/decoder RS(204,188), is the shortened length of the RS(255,239)
Reed-Solomon code. This shortened code is formed by 188 input data symbols,
plus 51 additional zero-padded symbols, before encoding with the RS(255,239).
The transmitted codeword doesn’t contain the padding sequence
which is rebuilt in RS decoder.
At the output of the RS coder, the data is left unchanged and the parity
codes are appended as shown in Fig.1. In this model, the parity codes
are transmitted first.
Fig.1: Codeword for systematic Reed-Solomon code

(1) Galois Field Arithmetic
Reed-Solomon codes are based on a specific area of
mathematics known as Galois Field, which is set up according to the
number of bits per symbol and the number of symbols per block (i.e.,
codeword). The elements of the Galois Field GF(2m)
are generated from the mth degree irreducible primitive
polynomial with the smallest number of terms. The primitive polynomial
of degree m can be written in the form:
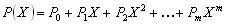 (1) (1)
Table I. List of primitive polynomials
The elements if Galois Field GF(2m)
can have two representations: power representation and polynomial representations.
Let a represent the root of the primitive
polynomial P(X). Each power representation ai,
where
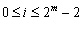 , ,
for elements of Galois Field GF(2m)
can be expressed as
 (2) (2)
where the binary vector {ai0, a1i, ..., ai,m-1}
is the polynomial representation of ai.
The power representation is convenient for multiplication and the polynomial
representation is convenient for addition.
m
|
|
m
|
|
3
|
1+X+X3
|
10
|
1+X3+X10
|
4
|
1+X+X4
|
11
|
1+X2+X11
|
5
|
1+X2+X5
|
12
|
1+X+X4+X6+X12
|
6
|
1+X+X6
|
13
|
1+X+X3+X4+X13
|
7
|
1+X3+X7
|
14
|
1+X+X6+X10+X14
|
8
|
1+X2+X3+X4+X8
|
15
|
1+X+X15
|
9
|
1+X4+X9
|
16
|
1+X+X3+X12+X16
|
(2) Generator polynomial
The generator polynomial of Reed-Solomon code is generally
defined as
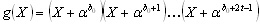 (3) (3)
where t is the correctable error number. For the special case
of b0 =1, the above equation will be simplified into
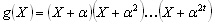 (4) (4)
The generator polynomial can also be expressed as a 2t order
of polynomial
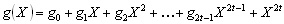 (5) (5)
(3) Encoding
2. In the Reed-Solomon code, all generated codewords
are exactly divisible by the generator polynomial. Let
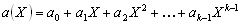 (6) (6)
be the input data to be encoded, where k= n-2t. The parity check
codes will be the coefficients of the remainder, b(X) = b0
+b1X +...+b2t-1X2t-1 resulting from
dividing the input data polynomial X2t a(X)
by the generator polynomial g(X). These parity codes are
then joined to the data symbols to form the transmitted codeword. The
RS encoding procedure can be accomplished by using a division circuit
as shown in Fig.2
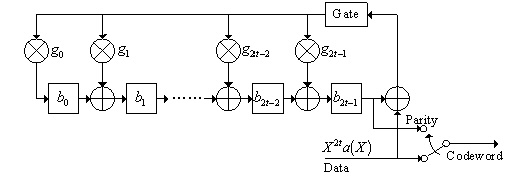
Fig.2 Encoding diagram for systematic Reed-Solomon
code
Netlist Form
RSCOD:NAME n1 n2 N=val K=val M =val
[B0 =val] [P0=val . . . PM=val] [RIN=val]
[ROUT=val]
Netlist Example
RSCOD:1 1 2 N=204 K=188 M =8 B0 =1 {P0,…P8}
= {1,0,1,1,1,0,0,0,1}
References
1. James J. Spilker, Digital Communications by
satellite, Prentice-Hall, 1977.
2. Shu Lin and D.J.Costello, Error Control Coding:
Fundamentals and applications, Prentice-Hall, 1983.
3. Y.Shayan, T.Le-Ngoc and V.Bhargava, “A
versatile time-domain Reed-Solomon decoder,” IEEE Journal
on Selected Areas in Communications, vol. 8, No.8, pp.1535-1542,
Oct. 1990.




HFSS视频教程
ADS视频教程
CST视频教程
Ansoft Designer 中文教程
|
|

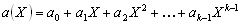 (6)
(6)