淘宝官方店推荐课程在线工具联系方式关于我们

	微波射频仿真设计 Ansoft Designer 中文培训教程 \| HFSS视频培训教程套装
	Agilent ADS 视频培训教程 \| CST微波工作室视频教程 \| AWR Microwave Office

首页 >> Ansoft Designer >> Ansoft Designer在线帮助文档

Ansoft Designer / Ansys Designer 在线帮助文档：

System Simulator >
System Component Models >
Equalizers >
Recursive Least Square Equalizer (RLSE)

Recursive Least Square Equalizer (RLSE)

Property	Description	Units	Default	Range/Type
NTAPS	The number of filter coefficients	None	4	(-Inf, Inf)/Integer
DELTA	Inverse correlation matrix initialization factor	None	0.0005	(-Inf, Inf)/Real
LAMBDA	Forgetting factor of the RLS algorithm	None	1	[0, 1]/Real
RIN1	Input1 impedance	Ohm	Inf	(0, Inf]/Real
RIN2	Input2 impedance	Ohm	Inf	(0, Inf]/Real
ROUT	Output impedance	Ohm	0	[0, Inf)/Real
Ports
Input1	The first input signal (real)
Input2	The second input signal (real)
Output	The output signal (real)

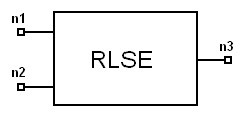
Notes

This model updates the filter coefficients of the equalizer based on the input signal and the error signal (i.e., the difference between the output of the equalizer and the actual desired output). The update is based on the recursive least square algorithm [1], [2].

Let X(n) and h(n) denote the input signal vector and the vector of the real filter coefficients respectively at time instant n. Each vector is assumed to be of length NTAPS (i.e., number
of filter taps). In addition, let K(n) denote the NTAPS x 1 Kalman gain vector and let the NTAPS x NTAPS inverse of the correlation matrix of the input signal be denoted by P(n).

The recursive least square algorithm is given by the following 5 steps:

1. Compute the filter output:

y(n) = tran(X(n)) * h(n-1

2. Compute the error:

e(n) = d(n) - y(n), where d(n) is the desired output

3. Compute the NTAPS x 1 Kalman gain vector:

K(n) = [P(n-1) * X(n)]/[LAMBDA + tran(X(n)) * P(n-1) * X(n)]

4. Update the inverse of the correlation matrix:

P(n) = (1/LAMBDA) [P(n-1) - K(n) * tran(X(n)) * P(n-1)]

5. Update the coefficients of the filter:

h(n) = h(n-1) + K(n) * e(n)

The following initial conditions are always assumed:

P(-1) = (1/DELTA) * I, where DELTA is a small positive number and I is the NTAPS x NTAPS identity matrix, e(-1) = 0, and h(-1) = 0.

Netlist Form

RLSE:NAME n1 n2 n3 NTAPS=val DELTA=val LAMBDA=val [RIN1=val] [RIN2=val] [ROUT=val]

Netlist Example

RLSE 1 2 3 NTAPS=8 DELTA=.005 LAMBDA=0.999

References

1. J. G. Proakis, Digital Communications, McGraw-Hill, 1989.

2. J. G. Proakis and D. G. Manolakis, Digital Signal Processing, Macmillan, 1988

HFSS视频教程 ADS视频教程 CST视频教程 Ansoft Designer 中文教程


Copyright © 2006 - 2013 微波EDA网, All Rights Reserved 业务联系：mweda@163.com