|
 Ansoft Designer / Ansys Designer 在线帮助文档: Ansoft Designer / Ansys Designer 在线帮助文档:
System Simulator >
System Component Models >
WCDMA Transmitter >
M-Sequence Generator (MSEQ)
M-Sequence Generator (MSEQ)
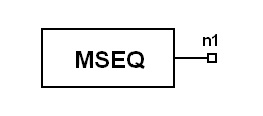
Notes
1. The m-sequence Generator model can be used to
generate m-sequence.
2. The m-sequence can be generated using Linear
Feedback Shift Register (LFSR) with a primitive polynomial[2].
For a given primitive polynomial, there are two methods[2]
of implementing LFSR, i.e, Galois feedback generator and Fibonacci
feedback generator. Since m-sequence has the maximum possible
period for a L-stage LFSR, it is also called maximal length sequence.
The maximum period of a L-stage LFSR can be proven to be 2L-1.
The structure of Linear Feedback Shift Register with Fibonacci feedback
generator is shown in Fig.1. The primitive polynomials g(D) is given
by
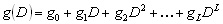 (1) (1)
3. Table I shows a list of primitive polynomials
for Linear Feedback Shift Register[2]. In the table, all
polynomials are specified by an octal number that defines the coefficients
of g(D). The octal number gives the coefficients of g(D) beginning with
go on the right and proceeding to gL in the last
nonzero position on the left. For example, a L-tage LFSR uses the entry
[367]. Expanding the octal entry 367 into binary form, we obtain
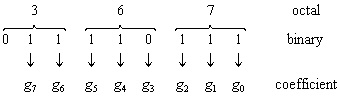
Therefore, 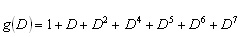
In Table I, each entry in brackets represents one primitive polynomial
as a series of octal numbers, explained in the above example.
The entries following by an asterisk correspond to circuit implementation
with only two feedback connections, which are very useful for high-speed
applications. No reciprocal polynomial is listed in Table I. Since the
reciprocal polynomial of a primitive polynomial is also primitive, each
entry in this table can be used to generate two distinct m-sequences.
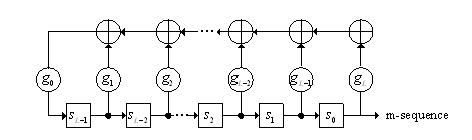
Fig. 1 Block diagram of m-sequence Generator (Fibonacci
feedback generator)
4. Note that the primitive polynomial in binary
is g0g1...gL and the initial state
of the shift register in binary is SL-1SL-2...S0
.
5. A list of primitive polynomials is tabulated
in the following table:
Degree
|
Octal Representation of
primitive polynomial (g0 on left to gLon
right)
|
2
|
[7]*
|
3
|
[13]*
|
4
|
[23]*
|
5
|
[45]*, [75], [67]
|
6
|
[103]*, [147], [155]
|
7
|
[211]*, [217], [235],
[367], [277], [325], [203]*, [313], [345]
|
8
|
[435], [551], [747], [453], [545],
[537], [703], [543]
|
9
|
[1021]*, [1131], [1461],
[1423], [1055], [1167], [1541],
[1333], [1605], [1751], [1743], [1617], [1553],
[1157]
|
10
|
[2011]*, [2415], [3771],
[2157], [3515], [2773], [2033],
[2443], [2461], [3023], [3543], [2745], [2431],
[3177]
|
11
|
[4055]*, [4445], [4215],
[4055], [6015], [7413], [4143],
[4563], [4053], [5023], [5623], [4577], [6233],
[6673]
|
12
|
[10123], [15647], [16533], [16047],
[11015], [14127],
[17673], [13565], [15341], [15053], [15621], [15321],
[11417], [13505]
|
13
|
[20033], [23261], [24623], [23517],
[30741], [21643],
[30171], [21277], [27777], [35051], [34723], [34047],
[32535], [31425]
|
14
|
[42103], [43333], [51761], [40503],
[77141], [62677],
[44103], [45145], [76303], [64457], [57231], [64167],
[60153], [55753]
|
15
|
[100003]*, [102043],
[110013], [102067], [104307], [100317],
[177775], [103451], [110075], [102061], [114725],
[103251],
[100021]*, [100201]*
|
16
|
[210013], [234313], [233303], [307107],
[307527], [306357],
[201735], [272201], [242413], [270155], [302157],
[210205],
[305667], [236107]
|
17
|
[400011]*, [400017],
[400431], [525251], [410117], [400731],
[411335], [444257], [600013], [403555], [525327],
[411077],
[400041]*, [400101]*
|
18
|
[1000201]*, [1000247],
[1002241], [1002441], [1100045],
[1000407], [1003011], [1020121], [1101005], [1000077],
[1001361], [1001567], [1001727], [1002777]
|
19
|
[2000047], [2000641], [2001441],
[2000107], [2000077],
[2000157], [2000175], [2000257], [2000677], [2000737],
[2001557], [2001637], [2005775], [2006677]
|
20
|
[4000011]*, [4001051],
[4004515], [6006031], [4442235]
|
21
|
[10000005]*, [10040205],
[10020045], [10040315], [10000635],
[10103075], [10050335], [10002135], [17000075]
|
Netlist Form
MSEQ:NAME n1 L=val [N =val] [PL=val]
[PH =val] [SL=val] [SH =val] NC=val [RC=val]
+ [T=val] [F =val] [ROUT=val]
Netlist Example
MSEQ:1 1 L = 5 N=31 PL = 41 PH = 0 SL = 31 SH =
0 NC = 124 RC = 1khz T= 1 F= 0
References
1. J. G. Proakis, Digital Communications, McGraw-Hill,
2001.
2. R. L. Peterson, R. E. Ziemer, and D. E. Borth,
Introduction to Spread Spectrum Communications.
Prentice Hall International Editions, 1995.




HFSS视频教程
ADS视频教程
CST视频教程
Ansoft Designer 中文教程
|
|
