|
 Ansoft Designer / Ansys Designer 在线帮助文档: Ansoft Designer / Ansys Designer 在线帮助文档:
System Simulator >
System Component Models >
Channels >
Multipath Rayleigh Fading Channel, Integer Delays (MRFCH)
Multipath Rayleigh Fading Channel, Integer
Delays (MRFCH)
Notes
1. This model can be used to simulate a Multipath
Rayleigh Fading Channel with Integer Delays in samples.
2. The Doppler power spectrum for Multipath Rayleigh
Fading Channel is given by [1][2]:
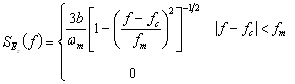 (1) (1)
where b is the average received power, fm
= wm/2p is the maximum Doppler shift given by
Vm/2l where
Vm is mobile velocity and l
is the wavelength of the transmitted signal at frequency fc.
3. Representing the RF channel as a time-variant
channel and using a base-band complex envelope representation,
the channel impulse response can be expressed as
 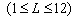 (2) (2)
where L is the number of paths, the amplitude ai(t)
for the ith path is a Rayleigh distributed random
variable, the phase shift fi
is uniformly distributed,ti >
= 0 is the channel delay. Since the Rayleigh fading processes ai(t) exp[(jfi(t)] is complex, the
in-phase process and quadrature process for each path are implemented
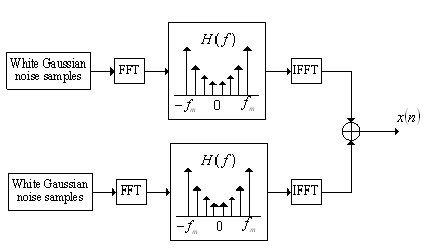
separately, as shown in Fig.1.
Fig. 1 Block diagram of Rayleigh fading simulator
Based on Eqn.(2), both the in-phase process and the quadrature process
can be generated by passing a White Gaussian noise process through
a baseband filter which has the following frequency response:
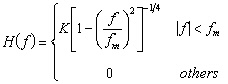 (3) (3)
where Kis constant to normalize the frequency response. The above
frequency response is generated in the frequency domain using
FFT with length = 2048 points. Each point (0 £ k £
length-1) corresponds to a certain frequency (fk)
by means of the following equation:
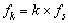 (4) (4)
where fs is the frequency sampling interval
typically chosen to be on the order of fm
/10.
The above frequency response has an even real part and an odd imaginary
part to guarantee that the filtering process will generate a real in-phase
and quadrature correlated Gaussian processes. Each two generated
Gaussian processes are combined to generate a Rayleigh fading process.
It is important to point out that whether in-phase process or quadrature
process is correlated among different points but the two processes
are generated independently and therefore, uncorrelated.
4. Assume that channel delay for each path can be expressed
by Di samples. Each generated Rayleigh
fading process corresponds to a path with a user-specified delay Di
and relative
power Pi, (0 £
i £ L-1). The expected
output along the ith fading path should be the input signal
delayed by Di samples and Rayleigh-faded with
the specified ith relative power Pi.
The total average power contribution from all paths is always normalized
to unity. This is accomplished by setting the standard deviation
of the ith generated in-phase and quadrature correlated
Gaussian processes to
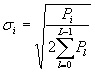 (5) (5)
These time series of the generated fading process is further increased
in the time domain to match the sampling rate of the input signal. This
is accomplished by linearly interpolating the fading process (i.e.,
inserting fading points between each two originally generated fading
points).
Netlist Form
MRFCH:NAME n1 n2 L=val VM=val [SEED=val]
D1=val P1=val [D2=val . . . P12=val]
[RIN=val] [ROUT=val]
Netlist Example
MRFCH:1 1 2 L=2 D1=0 P1=0 D2=2 P2=-2.0
References
1. W. C. Jakes, Microwave Mobile Communications,
New York: Wiley, 1974.
2. T. S. Rappaport, Wireless Communications: Principles
and Practice, Prentice-Hall, 1996.




HFSS视频教程
ADS视频教程
CST视频教程
Ansoft Designer 中文教程
|
|