![]()
![]()
|
Tetrahedral mesh: |
|
|
Frequency Domain General Purpose: |
|
|
Frequency Domain Resonant: |
|
|
Hexahedral mesh: |
|
|
Frequency Domain Resonant: |

Geometric Construction and Solver Settings
Introduction and Model Dimensions
Frequency Domain (fast resonant for sweep) with Tetrahedral mesh
Frequency Domain Solver (interpolative sweep) with Tetrahedral mesh
Resonant: fast S-parameter solver method with hexahedral mesh
In this tutorial you will learn how to simulate filter devices. As a typical example for a filter, you will analyze a Narrow Band Filter. The following explanations on how to model and analyze this device can be applied to other filter structures as well.
CST MICROWAVE STUDIO can provide a wide variety of results. This tutorial however, concentrates solely on the S-parameters of the filter.
We strongly suggest that you carefully read through the CST STUDIO SUITE Getting Started and CST MICROWAVE STUDIO Workflow and Solver Overview manual before starting this tutorial.
The following pictures show the structure and its initial dimensions in two different cross-sectional planes. The dimensions will be changed by means of local face modifications to demonstrate how existing structures can be modified and parametrized later on.
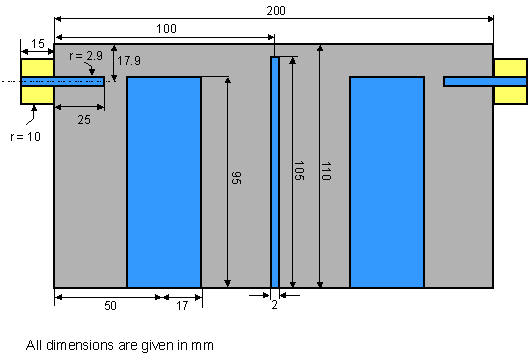
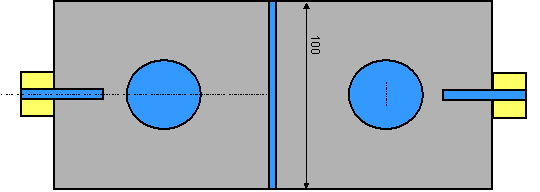
The structure consists of two resonators, each formed by a perfect electrically conducting cylinder in a rectangular cavity. Both resonators are coupled via a rectangular iris. The two coaxial ports are capacitively coupled to the device by extending the coaxial cables inner conductor into the resonators.
This tutorial will take you step by step through the construction of the model, and relevant screen shots will be provided so that you can double-check your entries along the way.
o Create a New Project
After launching the CST STUDIO SUITE
you will enter the start screen showing you a list of recently opened
projects and allowing you to specify the application which suits your
requirements best. The easiest way to get started is to configure a project
template which defines the basic settings that are meaningful for your
typical application. Therefore click on the Create
Project button ![]() in the New Project section.
in the New Project section.
Next you should choose the application area, which is Microwaves & RF for the example in this tutorial and then select the workflow by double-clicking on the corresponding entry.

For the filter structure, please select
Circuits & Components ![]() Waveguide & Cavity Filters
Waveguide & Cavity Filters ![]() Frequency Domain (fast resonant for sweep)
Frequency Domain (fast resonant for sweep) ![]() .
.
At last you are requested to select the units which fit your application best. For the filter structure, please leave the dimensions as follows:
|
Dimensions: |
mm |
|
Frequency: |
GHz |
|
Time: |
ns |
After clicking the Next button, you can give the project template a name and review a summary of your initial settings:

Finally click the Finish button to save the project template and to create a new project with appropriate settings. CST MICROWAVE STUDIO will be launched automatically due to the choice of the application area Microwaves & RF.
The template automatically sets the units to mm and GHz and the background material to be perfect electrically conducting (PEC.) In addition, the solver is optimized for resonant structures and the mesh settings for filter structures.
Please note: When you click again on the File: New and Recent you will see that the recently defined template appears below the Project Templates section. For further projects in the same application area you can simply click on this template entry to launch CST MICROWAVE STUDIO with useful basic settings. It is not necessary to define a new template each time. You are now able to start the software with reasonable initial settings quickly with just one click on the corresponding template.
Please
note: All settings made for a project template can be modified
later on during the construction of your model. For example, the units
can be modified in the units dialog box (Home:Settings ![]() Units
Units ![]() ) and the solver type can be selected
in the Home:Simulation
) and the solver type can be selected
in the Home:Simulation ![]() Start Simulation drop-down
list.
Start Simulation drop-down
list.
o Set the Working Planes Properties
After the units have been correctly
set (which has been done by the template here), the modeling process usually
starts with setting the working planes size large enough for the device.
Because the structure has an extension of 200 mm along one coordinate
direction, the working planes size should be set to 200 mm (or more).
These settings can be changed in a dialog box that opens after selecting
View:Visibility
![]() Working Plane
Working Plane ![]()
![]() Working Plane Properties.
Please note that we will use
the same document conventions here as introduced in the Workflow and Solver Overview
manual.
Working Plane Properties.
Please note that we will use
the same document conventions here as introduced in the Workflow and Solver Overview
manual.
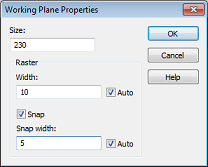
In this dialog box, you should set the Size to 230 (the unit that has been previously set to mm is displayed in the status bar), the Raster Width to 10 and the Snap width to 5 to obtain a reasonably spaced grid. Please confirm these settings by pressing the OK button.
o Draw the Filters Housing
Because the background material has been set to PEC, you need to model only the interior of the filter. The structure will then be automatically embedded within a perfect electrically conducting enclosure.
Therefore, you should start the structure
modeling by entering the filters housing that can easily be defined by
creating an air-brick. Please activate the brick creation tool now
by selecting
Modeling:
Shapes ![]() Brick
Brick ![]() .
.
When you are prompted to enter the first point, you may enter the coordinates numerically by pressing the TAB key that will open the following dialog box:
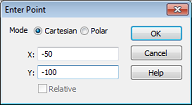
In this example you should create the housing with the transversal extension of 100 x 200 mm. In order to model the structure symmetrically to the origin, you should now enter the coordinates X = -50 and Y = -100 in the dialog box and press the OK button (please remember that the geometric unit is currently set to mm).
The next step is to enter the opposite corner of the bricks base: Press the TAB key again and enter X = 50, Y = 100 in the coordinate fields before pressing OK.
You will now be requested to enter the height of the brick. This can also be achieved by pressing the Tab key, entering a Height of 110 and pressing the OK button again.
After the steps above have been completed, the following dialog box will appear, displaying a summary of your input:
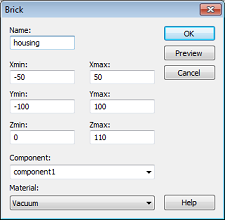
Please check all entries carefully. If you encounter any mistakes, please change the value in the corresponding entry field.
You should then give the shape a meaningful Name (e.g. housing). Because the housing consists of vacuum, you can keep the Material default setting (Vacuum) as well as the assignment to the default Component component1.
Please note: The use of different components allows you to combine several solids into specific groups, independently of their material behavior. However, in this tutorial it is convenient to construct the complete filter device as a representation of one component.
Finally, confirm the creation by pressing OK. Your screen should now look as follows (you can press the Space key in order to zoom the structure to the maximum possible extent):

Because structures will be inserted
into this air brick in the following steps, it is advantageous to switch
the display to wireframe mode because otherwise the newly created shapes
may be hidden inside the brick. The easiest method of activating
the wireframe visualization mode is to select
View: Visibility ![]() Wire Frame
Wire Frame ![]() or use the corresponding shortcut: Ctrl+w. The structure should
now look as follows:
or use the corresponding shortcut: Ctrl+w. The structure should
now look as follows:

o Create the Cylindrical Resonators
The next step is to create the cylindrical
resonators inside the air brick. Please activate the cylinder creation
tool by selecting
Modeling:
Shapes
![]() Cylinder
Cylinder ![]() .
.
The first step in the cylinder creation process is to enter the center point coordinates. This can be achieved numerically by pressing the Tab key and entering the dimensions X = 0, Y = -50 in the dialog box before pressing the OK button. In the following sections, we will assume that you always confirm the settings in a dialog box by pressing the OK button unless mentioned otherwise.
The second step in the cylinders creation is to specify the outer radius. Similar to the procedure above, you should now set the Radius to 17 after pressing the Tab key.
After pressing the Tab key once more and setting the Height to 95, you may skip the definition of the cylinders inner radius by pressing the Esc key. Finally, the following dialog box will appear:
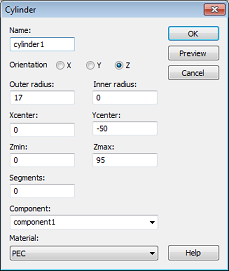
Please check and correct all settings as necessary before specifying the cylinders Name as cylinder1. To this point, the cylinder consists of vacuum material. However, to specify the cylinder to be a perfect electrical conductor (PEC), you must change the Material assignment to PEC. Because the filter is constructed as one component, you can skip the Component setting and confirm the creation of the cylinder by pressing the OK button.
Your screen should then look as follows:
After successfully creating the first cylinder you can now model the second cylinder in the same manner:
1.
Activate the cylinder tool:
Modeling:
Shapes
![]() Cylinder
Cylinder ![]() .
.
2. Press the Tab key and set the centers coordinates to X = 0, Y = 50.
3. Press the Tab key and set the Radius to 17.
4. Press the Tab key and set the Height to 95.
5. Press the Esc key to skip the definition of the inner radius.
6. Set the Name of the cylinder to cylinder2
7. Keep the Material assignment as PEC and press the OK button.
After the successful creation of the second cylinder, the screen should then look as follows:

Please note: The creation of the second cylinder could also be achieved by applying a transformation to the first one. For the sake of simplicity, we recommended that you draw the cylinder twice. The application of transformations to copy shapes will be explained later in this tutorial.
o Create the Iris between the two Cavities
The next step is to create the rectangular iris between the two cavities. This could easily be achieved by entering its dimensions numerically in the same manner as the creation of the air brick above. However, because the iris should always extend across the entire width of the filter, we will now explain how this can be forced using picked points.
After activating the brick creation
tool by selecting
Modeling:
Shapes ![]() Brick
Brick ![]() ,
you are requested to enter the first point. Instead of entering
the point by double-clicking with the mouse or entering the point numerically
by pressing the Tab key, you should now activate the pick edge center
tool (
Modeling:
Picks
,
you are requested to enter the first point. Instead of entering
the point by double-clicking with the mouse or entering the point numerically
by pressing the Tab key, you should now activate the pick edge center
tool (
Modeling:
Picks
![]() Pick Point
Pick Point ![]() Pick Edge Center
Pick Edge Center ![]() or use the shortcut M).
Afterwards, all straight edges will
be highlighted in the model:
or use the shortcut M).
Afterwards, all straight edges will
be highlighted in the model:
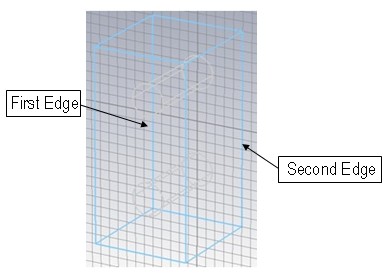
Double-click on the first edge shown in the picture above. By moving the mouse pointer you can now confirm that the first point of the brick is aligned with the mid-point of this edge. Even if the location of the edge center changes (e.g. by parametrically editing the structure), the first point of the newly created brick will always be linked with the edge center's current position.
You should now repeat the same steps (activate pick edge center tool, double-click on the edge) with the second edge to specify the bricks second point.
Because both points are now located on a line, the brick creation tool prompts for the width of the brick. You should now press the Tab key and set the Width of the brick to 2.
In the last step of the interactive brick creation you are requested to enter the bricks height. This can also be accomplished by pressing Tab and setting the Height to 105. Completing this step will open the following dialog box:
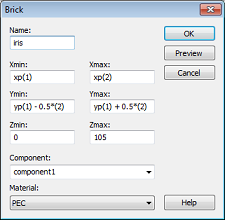
Some of the entry fields now contain expressions that reflect the relative construction of the brick. The expression xp(1), for instance, represents the x-coordinate of the initially picked edge's center.
Set the Name of the brick to iris and the Material assignment to PEC, then press the OK button. Your model should now look as follows:
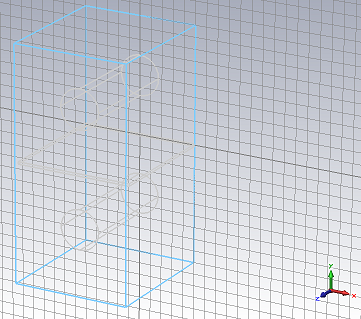
o Create the Coaxial Couplings
To this point, you have modeled the filters internal structure. However, the next step is to model the coaxial couplings on both side walls of the filter.
Before you begin modeling the cylinders,
you should first align the working coordinate system with one of the side
walls of the filter. This will allow you to model the coupling structure
in a more convenient way. Please deactivate the wireframe plot mode
by deselecting
View: Visibility ![]() Wire Frame
Wire Frame ![]() , or use the corresponding shortcut Ctrl+w.
, or use the corresponding shortcut Ctrl+w.
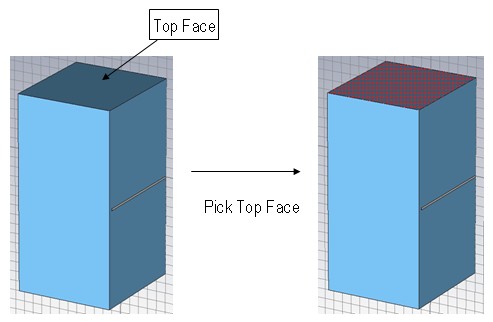
Please activate the smart pick tool by selecting
Modeling: Picks ![]() Picks
Picks ![]()
![]() Pick
Point, Edge or Face (shortcut S.) Now, you can double-click on the top face to
select it as shown above. The selected face should then be highlighted
in the model (see picture above).
Pick
Point, Edge or Face (shortcut S.) Now, you can double-click on the top face to
select it as shown above. The selected face should then be highlighted
in the model (see picture above).
The next step is to align the working
coordinate system with the picked face by selecting either
Modeling:
WCS ![]() Align WCS
Align WCS ![]() or using shortcut w.
or using shortcut w.
After activating the wireframe drawing mode again (Ctrl+w), the model should look as follows:
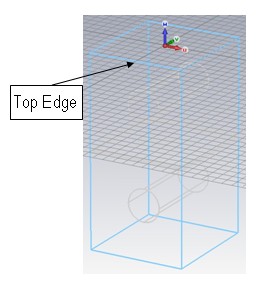
The location of the coaxial couplers center is located 17.9 mm below the top wall of the filter. Therefore, the next step is to align the working coordinate system with the top wall of the filter, which will make the definition of the couplers location more convenient.
You should now again activate the
pick edge center tool (
Modeling:
Picks
![]() Pick Point
Pick Point ![]() Pick Edge Center
Pick Edge Center ![]() or use the shortcut M
) and double-click on the top edge shown in
the above picture. Now the center point of this edge should become highlighted.
You can then align the origin of the working coordinate system with this
point by selecting
Modeling:
WCS
or use the shortcut M
) and double-click on the top edge shown in
the above picture. Now the center point of this edge should become highlighted.
You can then align the origin of the working coordinate system with this
point by selecting
Modeling:
WCS ![]() Align WCS
Align WCS ![]() or using shortcut w. The following picture shows the
new location of the working coordinate system:
or using shortcut w. The following picture shows the
new location of the working coordinate system:
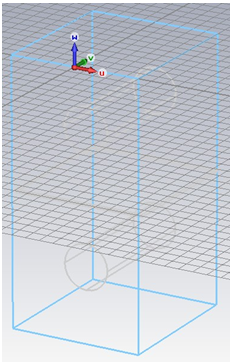
With the working coordinate system aligned this way, the construction of the coaxial coupler is straightforward:
1.
Activate the cylinder tool:
Modeling:
Shapes
![]() Cylinder
Cylinder ![]() .
.
2. Press the Tab key and set the centers coordinates to U = 0, V = 17.9.
3. Press the Tab key and set the Radius to 10.
4. Press the Tab key and set the Height to 15.
5. Press the Esc key to skip the definition of the inner radius.
6. Set the Name of the cylinder to coaxial substrate.
The cylinder creation dialog box should then look as follows:
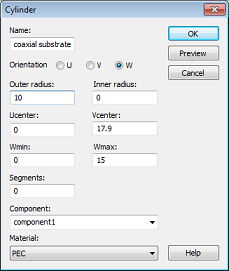
You still need to define the substrate material. Because no material has yet been defined for the substrate, open the material definition dialog box by selecting [New Material...] in the Material dropdown list:
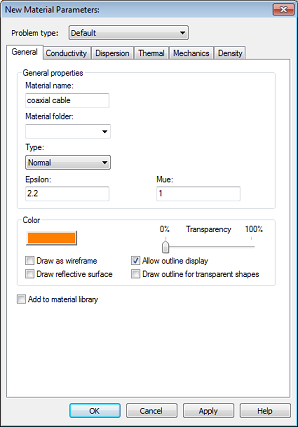
In this dialog box, you should first define a new Material name (e.g. coaxial cable) and set the Type to a Normal dielectric material. Then specify the material properties in the Epsilon and Mue fields. Here, you only need to change the dielectric constant Epsilon to 2.2. Finally, select a color for the layer by pressing the Change button. Your dialog box should now look similar to the above picture before you press the OK button.
Please note: The defined material coaxial cable will now be available inside the current project for the creation of other solids. However, if you also want to save this specific material definition for other projects, you may check the button Add to material library. You will have access to this material database by clicking on Load from Material Library in the Materials context menu in the navigation tree.
Back in the cylinder creation dialog box you can also press the OK button to finally create the coaxial couplers substrate. Your model should now look as follows:
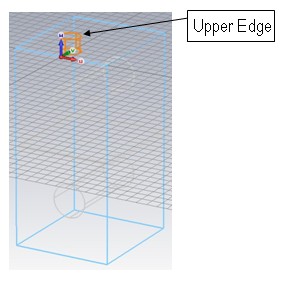
The next step is to model the inner conductor of the coaxial coupler as a perfect electrically conducting cylinder. Because both cylinders should always be coaxial, it is convenient to move the local coordinate system to the center of the substrate cylinder.
Therefore, activate the circle center
pick tool by either selecting
Modeling:
Picks
![]() Pick Point
Pick Point ![]() Pick Circle Center
Pick Circle Center ![]() or use the shortcut C.
Now double-click on the substrate
cylinders upper edge as shown in the above picture which will highlight
the circle center point. Finally, align the working coordinate system
with this point by selecting
Modeling:
WCS
or use the shortcut C.
Now double-click on the substrate
cylinders upper edge as shown in the above picture which will highlight
the circle center point. Finally, align the working coordinate system
with this point by selecting
Modeling:
WCS ![]() Align WCS
Align WCS ![]() or using shortcut w. The following picture shows how your
model should now look:
or using shortcut w. The following picture shows how your
model should now look:
The inner conductor of the coaxial connector can now be easily modeled by performing the following operations to create a cylinder:
1.
Activate the cylinder tool:
Modeling:
Shapes
![]() Cylinder
Cylinder ![]() .
.
2. Press the Tab key and set the centers coordinates to U = 0, V = 0.
3. Press the Tab key and set the Radius to 2.9.
4. Press the Tab key and set the Height to -40.
5. Press the Esc key to skip the definition of the inner radius.
6. Set the Name of the cylinder to conductor.
7. Change the Material to perfect electric conducting (PEC).
8. Press the OK button to finally create the cylinder.
The next step is to deactivate the working
coordinate system by deselecting
Modeling:
WCS ![]() Local
WCS
Local
WCS ![]() .
After completion of these steps, the model should now look as follows:
.
After completion of these steps, the model should now look as follows:

To this point, you have modeled one
coaxial coupler but still need to create the second coupler. This
is most conveniently achieved by creating a mirrored copy using an appropriate
shape transformation. With help of multiple selections, this must
be done only once for the complete coaxial coupler. Please select
both parts of the connector in the navigation tree (located at Components ![]() component1
component1 ![]() coaxial substrate and Components
coaxial substrate and Components
![]() component1
component1
![]() conductor)
while holding the Ctrl key.
conductor)
while holding the Ctrl key.
Afterwards, open the shape transformation
dialog box (
Modeling:
Tools ![]() Transform
Transform ![]() Mirror
Mirror
![]() ):
):
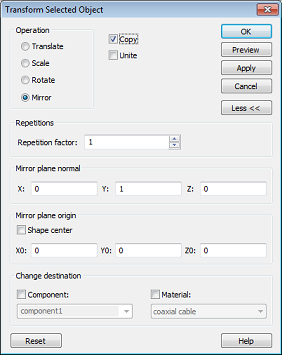
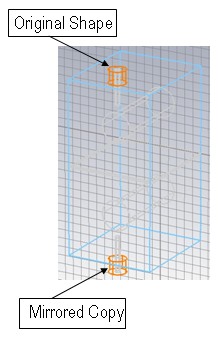
The first action in this dialog is to set the Operation to Mirror. Then the parameters of the mirror plane are specified. Because this plane should be the XZ plane of the global coordinate system, you only need to set the Y coordinate of the Mirror plane normal to 1. To create a mirrored copy of the existing multiple selected shape, please enable the option Copy. The newly created solids will then also be grouped to the existing component component1. Confirm the settings by pressing OK.
You end up with the following picture:
o Define Ports
The next step is to add the ports to the filter for which the S-parameters will be calculated. Each port will simulate an infinitely long waveguide (here a coaxial cable) that is connected to the structure at the ports plane. Waveguide ports are the most accurate way to calculate the S-parameters of filters and should thus be used here.
Because a waveguide port is based on the two dimensional mode patterns in the waveguides cross-section, it must be defined large enough to entirely cover these mode fields. In the case of a coaxial cable, the port therefore must cover the coaxial cables substrate completely.
Before you continue with the port definition,
please deactivate the wireframe plot mode by deselecting
View: Visibility ![]() Wire Frame
Wire Frame ![]() , or use the corresponding shortcut Ctrl+w.
, or use the corresponding shortcut Ctrl+w.
The ports extent can either be defined
numerically or, more conveniently, by picking the face to be covered by
the port. Therefore, please activate the smart pick tool (
Modeling: Picks ![]() Picks
Picks ![]()
![]() Pick
Point, Edge or Face , shortcut S
) and double-click
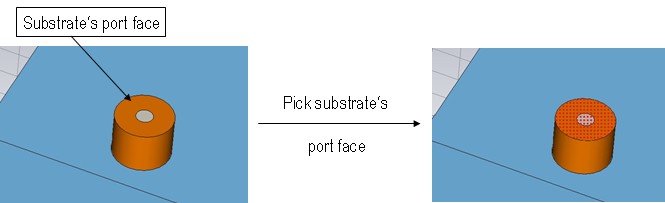
on the substrates port face on one of the coaxial couplers as shown below:
Pick
Point, Edge or Face , shortcut S
) and double-click
on the substrates port face on one of the coaxial couplers as shown below:
Please now open the waveguide dialog
box (
Simulation:
Sources
and Loads ![]() Waveguide Port
Waveguide Port ![]() ) to define port 1:
) to define port 1:
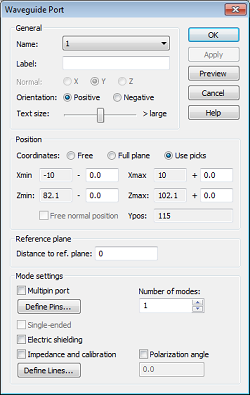
Whenever a face is picked before the port dialog is opened, the picked faces extent will automatically define the ports location and size. Thus, the ports Position is initially set to Use picks for the coordinates. You can simply accept this setting.
The next step is to choose the number of modes to be considered by the port. For coaxial devices, we usually have only a single propagating mode. You should therefore keep the default of one mode.
Finally, check the settings in the dialog box and press the OK button to create the port:
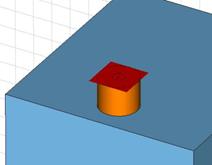
Now you can repeat the same steps for the definition of port 2.
1.
Pick the corresponding substrates port face (
Modeling: Picks ![]() Picks
Picks ![]()
![]() Pick
Point, Edge or Face , shortcut S
).
Pick
Point, Edge or Face , shortcut S
).
2.
Open the waveguide dialog box (
Simulation:
Sources
and Loads ![]() Waveguide Port
Waveguide Port ![]() ).
).
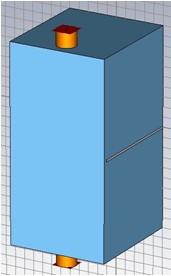
3. Press OK to store the ports settings.
Your model should now look as follows:
o Define Boundary Conditions and Symmetries
Always check the boundary and symmetry
conditions before starting the solver. Enter the boundary definition mode by selecting
Simulation:
Settings ![]() Boundaries
Boundaries ![]() . The boundary conditions will
then become visualized in the main view as follows:
. The boundary conditions will
then become visualized in the main view as follows:
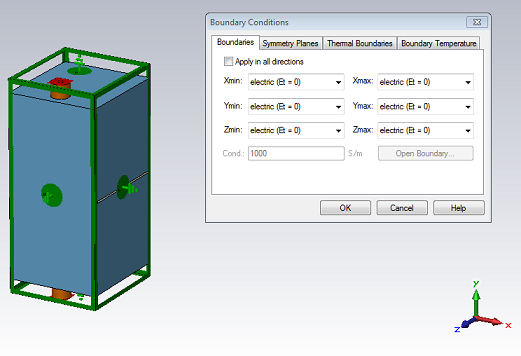
Here, all boundary conditions are set to electric, which means that the structure is embedded in a perfect electrically conducting housing. These defaults (that have been set by the template) are appropriate for this example.
Due to the structure's symmetry about the YZ plane and the fact that the magnetic field in the coaxial cable is perpendicular to this plane, a symmetry condition can be used. This symmetry will reduce the time required for the simulation considerably. Please refer to the example in the Workflow and Solver Overview manual for more information on symmetry conditions.
Please enter the symmetry plane definition mode by activating the Symmetry planes tab in the dialog box.
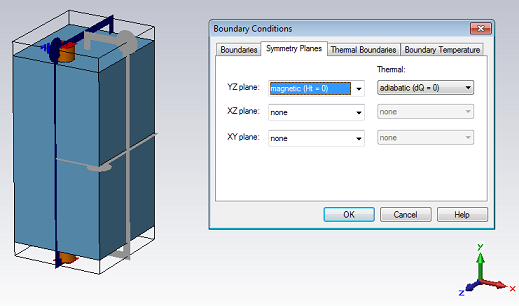
By setting the symmetry plane YZ to magnetic, you force the solver to calculate only the modes that have no tangential magnetic field component to these planes (thus forcing the electric field to be tangential to these planes).
Finally press the OK button to complete this step.
In general, you should always make use of symmetry conditions whenever possible to minimize calculation times.
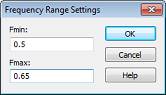
o Define the Frequency Range
The frequency range for this example
extends from 0.5 GHz to 0.65 GHz. Change Fmin and Fmax
to the desired values in the Frequency Range Settings dialog box (that
is opened by pressing
Simulation:
Settings
![]() Frequency
Frequency
![]() ) and store these settings by pressing the OK
button (the frequency unit which has previously been set to GHz is shown
in the status bar).
) and store these settings by pressing the OK
button (the frequency unit which has previously been set to GHz is shown
in the status bar).
o Apply Local Face Modifications
One way to introduce parameters in an
existing structure is to use local face modifications. As all changes
will be applied to PEC faces hereafter, select Materials ![]() PEC from
the navigation tree to plot all solids other than PEC solids transparently.
The local face modifications are available from
Modeling:
Tools
PEC from
the navigation tree to plot all solids other than PEC solids transparently.
The local face modifications are available from
Modeling:
Tools ![]() Modify Locally
Modify Locally ![]() .
.
Select the top face of the iris as highlighted in red in the screen shot below.
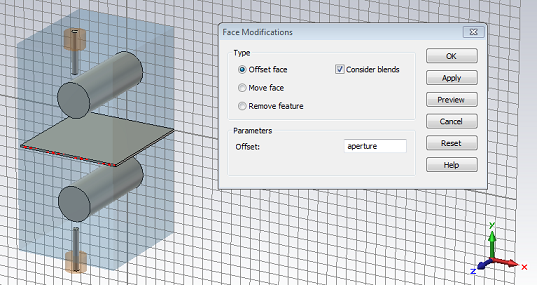
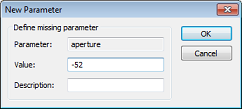
Enter a new parameter named aperture as the value for the offset and press OK. A prompt will be displayed, asking for the value (set to -52) of the parameter aperture.
Likewise, offset the circular faces of the coaxial lines' inner conductors (those faces which are located inside the housing.)
Enter a new parameter named Input_Coupling1 as the value for the offset for the face of conductor_1. Again, a prompt will be displayed, asking for the value (which is set to 6.3) of the new parameter.

The same offset is applied to the solid named conductor. Enter a new parameter Input_Coupling equal to 6.3 for the face's offset.
With everything but PEC drawn transparent, the filter now should look like this when viewed from the side:
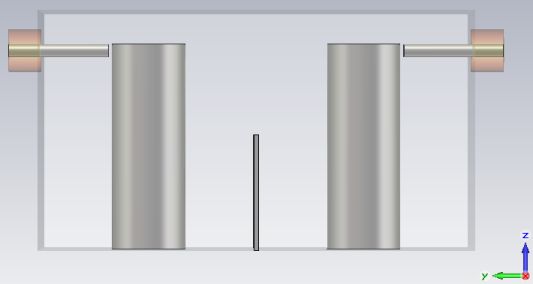
o Define Face Constraints for Sensitivity Analysis
The derivative of S-parameters with respect to a change of material parameters or geometric
parameters is the result of the sensitivity analysis that can be performed for instance with the Frequency Domain solver.
We define face constraints in order to prepare the sensitivity analysis for small geometric modifications, very similar
to introducing parameters by local face modifications.
The face constraints are available from
Modeling:
Tools ![]() Modify Locally
Modify Locally ![]() Define Face Constraints
Define Face Constraints ![]() .
.
Select the top face of the iris as highlighted in red in the screen shot below.

The value 53 is the distance of the selected face to the plane z=0. Click on parametrize. A prompt will be displayed: enter a new parameter named iris with the value left unchanged and press OK.
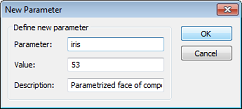
After completing the above steps, you are ready to start the S-parameter computation. The filter device analyzed here is a narrow band filter for which four different solution methods can be used:
1. Transient solver
2. Frequency domain solver: General Purpose
3. Frequency domain solver: Resonant: Fast S-Parameter
4. Frequency domain solver: Resonant: S-Parameter, fields
The transient solver is the most versatile tool to solve any kind of S-parameter problem. However, for strongly resonant structures (such as the filter demonstrated here), the frequency domain solvers provide an interesting alternative that can be computationally more efficient than the transient solver. Consequently, in this chapter you will learn how to use two different types of frequency domain solvers to analyze the device. Please refer to the Workflow and Solver Overview manual and the other tutorials on how to utilize the transient solver for S-parameter problems.
Please note that during the creation of the new project the Frequency Domain (fast resonant for sweep) with the default tetrahedral mesh has been pre-selected as the most appropriate solver for the given application. It is a combination of the general purpose Frequency Domain solver's adaptive mesh refinement followed by the Resonant: Fast S-parameter sweep. This choice is described in the first section.

In the second section the simulation is still performed with the Frequency Domain solver and tetrahedral mesh but with the interpolative S-parameter sweep.
The third section describes the Resonant: fast S-parameter solver method with hexahedral mesh. Two completely different approaches to solving the problem provide proof of the simulations reliability. Both sections are self-contained parts and it is sufficient to work through only one of them, depending on what solver you are interested in. The chapter ends with a comparison of the two methods.
Please note: Some solvers may not be available to you due to license restrictions. Please contact your sales office for more information.
The Frequency Domain Solver Parameters dialog box is opened by selecting
Home:
Simulation ![]() Start Simulation
Start Simulation
![]() .
.
The ![]() reflects the pre-selection of the solver by the project template, which can also be selected
by the drop down menu
Home:
Simulation
reflects the pre-selection of the solver by the project template, which can also be selected
by the drop down menu
Home:
Simulation ![]() Start Simulation
Start Simulation ![]() Frequency
Domain Solver
Frequency
Domain Solver ![]() if necessary.
if necessary.
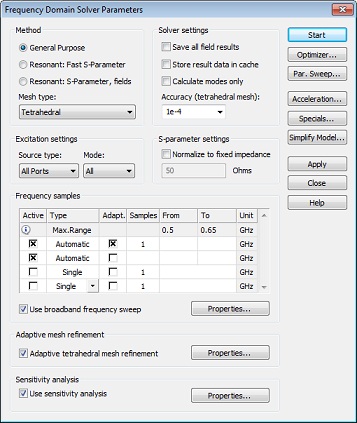
Please activate the sensitivity analysis and select Properties to verify that the parameter iris will be used for the S-parameter sensitivity analysis:
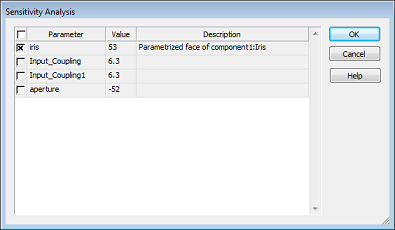
Close the sensitivity analysis dialog by pressing OK, check your settings in the dialog box and press the Start button. A progress bar and messages will be shown, keeping you informed about the current status of your calculation.
To review
the solver time required to achieve these results, you can display the
solver log-file by selecting
Simulation:
Solver
![]() Logfile
Logfile ![]() . Please scroll
down the text to obtain the following timing information (the actual values
may vary depending on the speed of your computer):
. Please scroll
down the text to obtain the following timing information (the actual values
may vary depending on the speed of your computer):
Mesh generation time : 0 s
Mesh adaptation time : 94 s (= 0 h, 01 m, 34 s)
Fast resonant solver : 18 s
Total Solver Time : 112 s (= 0 h, 01 m, 52 s)
--------------------------------------------------------------------------------
Congratulations, you have simulated the Narrow Band Filter! Lets review the results.
o 1D Results (S-Parameters and S-parameter sensitivity)
The S-Parameters
can be plotted by clicking on the 1D Results ![]() S-Parameters folder.
S-Parameters folder.
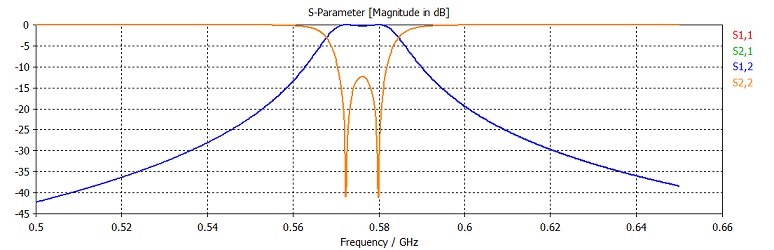
As expected, the bandwidth of the transmission S2,1 is quite small.
Furthermore, the S-parameters at about 0.57 GHz are most sensitive to
changes of the iris height, as can be seen from the 1D Results ![]() S-Parameter Sensitivity
S-Parameter Sensitivity![]() iris folder.
iris folder.
o 2D Results (Port Modes)
The port modes can be easily displayed by opening the
2D/3D Results
![]() Port Modes
Port Modes ![]() Port1
folder from the navigation tree. To visualize the electric field
of the fundamental port mode, click on the e1 folder.
Port1
folder from the navigation tree. To visualize the electric field
of the fundamental port mode, click on the e1 folder.
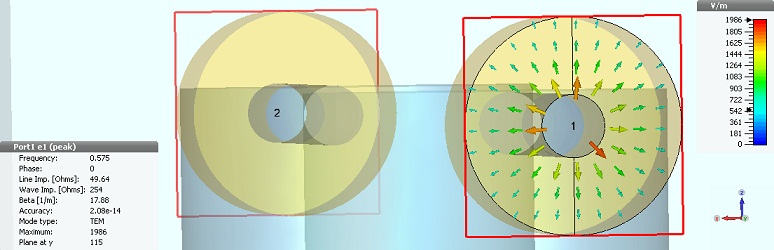
The plot also shows some important properties of the mode, such as mode type, propagation constant and line impedance. The port modes at the second port can be visualized in the same manner.
o Accuracy Considerations
The frequency domain solver modules are mainly affected by two sources of numerical inaccuracies:
1. Numerical errors introduced by the linear equation system solvers.
2. Inaccuracies arising from the finite mesh resolution.
In the following sections we provide hints on how to minimize these errors and achieve highly accurate results.
The first type of error is always quantified as Accuracy for the solution of a linear equation system. Decreasing this number improves the accuracy of the solutions. The default value of 1e-4 for the Frequency Domain solver with tetrahedral mesh is usually sufficient.
The inaccuracies arising from the finite mesh resolution are usually more difficult to estimate. The only way to ensure the accuracy of the solution is to increase the mesh resolution and recalculate the S-parameters. When the desired results no longer significantly change as the mesh density is increased, then convergence has been achieved.
In the example above, you have used the default mesh adaptation settings. The solver output possibly displays a warning telling that the "Mesh adaptation terminated because the maximum number of passes is reached."
You can visualize
the maximum relative difference of the S-parameters for two subsequent
passes by selecting 1D Results ![]() Adaptive Meshing
Adaptive Meshing ![]() f=0.575
f=0.575 ![]() Delta S from the navigation tree:
Delta S from the navigation tree:

Please note that the S-parameter variation between the seventh and the eighth mesh adaptation pass is already below the
default threshold of 0.01 but just for the first time. The check is by default performed twice because the difference
between passes does not necessarily decrease with the number of mesh adaptation passes.
Instead of increasing the number of mesh adaptation passes and recalculating all results, the solver can just continue
the adaptive mesh refinement.
Open the Frequency Domain Solver Parameters dialog box again by selecting
Home:
Simulation ![]() Start Simulation
Start Simulation
![]() and press the Start button to continue the mesh refinement. The S-parameters slightly change as the adaptive
mesh refinement is continued, but finally are very similar to those results obtained after eight passes.
and press the Start button to continue the mesh refinement. The S-parameters slightly change as the adaptive
mesh refinement is continued, but finally are very similar to those results obtained after eight passes.
Please note that the solver settings still can be improved for this example, as can be concluded from the message output window. It shows that the first adaptation frequency at 0.65 GHz was skipped because an S-parameter check revealed that the frequency seemed to be in the stop band of the filter:
![]()
You can click on the hyperlink More in the message window to open the online help page with further explanation.
How to avoid this calculation is exaplained in the section Adaptive mesh refinement settings hereafter.
o Making a Copy of the Previous Solver Results
Before performing the simulation with another frequency domain solver, you may want to keep the previous results to compare the two simulations. To obtain the copy of the current results: Select, for example, the S-Parameters folder in 1D Results, then press Ctrl+c and Ctrl+v. The copies of the results will be created in the selected folder. The names of the copies will be S1,1_1, S2,1_1 etc. You may rename them to S1,1_RF, S2,1_RF and so on using the Rename command from the context menu.
o Adaptive mesh refinement settings
Because the General Purpose frequency domain solver with tetrahedral mesh runs the adaptive mesh refinement at individual frequency samples, the adaptation frequency should be moved to the pass band of the filter. From the previous solver run using the Resonant: Fast S-Parameter solver, we know that the center of the pass band is close to 0.575 GHz. By default, the adaptation frequency is automatically chosen as the uppermost frequency of the global frequency range.
The adaptive mesh refinement settings for the filter thus can be improved, as was also mentioned in the previous section.
To avoid the first calculation being performed in the stop band, open the solver dialog again by selecting
Home:
Simulation ![]() Start Simulation
Start Simulation
![]() ,
change the Type of the mesh refinement frequency sample (the one which has the Adapt. column checked) to Single and enter the fixed frequency 0.575 GHz:
,
change the Type of the mesh refinement frequency sample (the one which has the Adapt. column checked) to Single and enter the fixed frequency 0.575 GHz:

Note that the single frequency adaptive mesh refinement is already activated for the general purpose frequency domain solver with tetrahedral mesh. The broadband frequency sweep is enabled, and the default sampling strategy is given by the row after the adaptation frequency: The Automatic type is selected, and therefore an adaptive frequency sampling strategy is employed (rather than equidistant or logarithmic sampling.) No number of samples is specified, meaning that the solver will calculate as many samples as necessary in order to satisfy the S-parameter sweeps convergence criterion. The From and To fields are left blank as well, indicating that the global frequency range will be used, as shown in the Max. Range line.
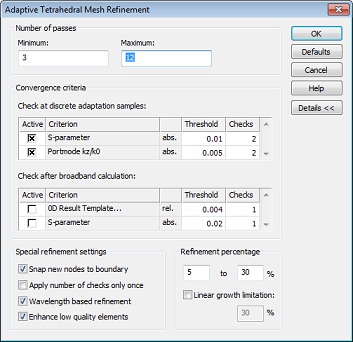
As can be concluded from the previous results, the number of mesh adaptation passes should be increased for subsequent solver runs. Please click on Properties in the Adaptive Mesh Refinement frame to open the adaptive tetrahedral mesh refinement settings dialog box. Enter for instance 12 as the maximum number of passes. Please also expand the Details and deactivate the Linear growth limitation in the Refinement percentage frame to allow the mesh to grow faster, then confirm the changes and close the dialog by pressing OK:
o Broadband sweep settings
Now the General Purpose frequency domain solver will be used with interpolative sweep rather than with the fast resonant sweep for the S-parameter calculations. Click on Properties next to Use broadband frequency sweep. The Frequency Domain Solver Sampling dialog shows the Interpolative frequency sweep properties at the top and the option for the Resonant: Fast S-parameter sweep properties at the bottom. In the latter frame, please deactivate Run after adaptive mesh refinement if applicable. Afterwards, close the dialog by pressing OK.

In the frequency domain solver parameters dialog, please press the Start button. The choice to keep the mesh from the previous calculation will be offered, but for now select Delete all to start the adaptive mesh refinement from the beginning.
The solver first performs the adaptive mesh refinement at 0.575 GHz. Afterwards, the interpolative broadband S-parameter sweep adaptively chooses additional frequency samples to obtain the full frequency-dependent S-parameter matrix. A few progress bars are running, keeping you informed about the current status of your calculation (e.g. tetrahedral mesh generation, port mode calculation ...).
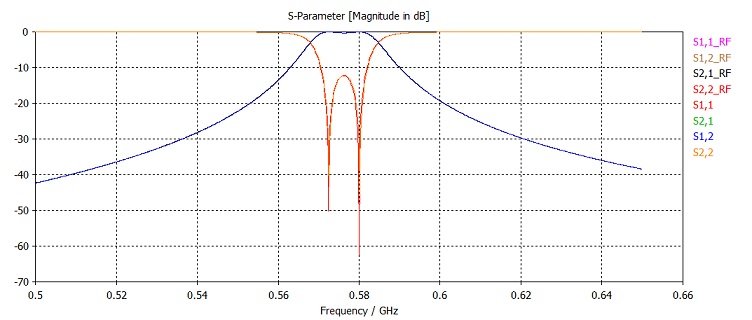
The solver will finish after a short time and deliver results that show only a slight deviation compared to the Resonant: Fast S-Parameter sweep used previously, whose S-parameters are marked by _RF:
o Invoke a Field Calculation from the S-Parameter Curve
With the general purpose solver you may calculate fields at
certain frequencies. This can be done by using Monitors.
Field monitors are usually set up before the first or a continued solver
run (for more information see the Workflow
and Solver Overview manual.)
The general purpose frequency domain solvers offer another convenient
way to calculate the E, H, D, or B fields at a single frequency using
the the axis marker: click for instance on the 1D Results ![]() S-Parameters
S-Parameters
![]() S1,1 item
in the navigation tree. Then select the axis marker by
1D Plot:
Markers
S1,1 item
in the navigation tree. Then select the axis marker by
1D Plot:
Markers
![]() Axis
Marker
Axis
Marker
![]() Change
Position
or by pressing the right mouse button and selecting the Axis Marker option from the context menu.
Change
Position
or by pressing the right mouse button and selecting the Axis Marker option from the context menu.
In the following dialog, please enter the frequency value where you would like to calculate the fields, for instance at 0.575 GHz, which had been chosen as the adaptive mesh refinement frequency inside the pass band.
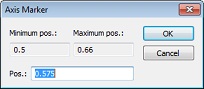
Confirm the setting by pressing OK.
If you would like to observe where
the frequency domain solver has actually placed the frequency samples,
you can select
1D Plot:
Plot Properties
![]() Properties
Properties
![]() Curve Style
or just Curve Style from the context menu. Select S1,1 only and choose Additional marks in the Marker style frame:
Curve Style
or just Curve Style from the context menu. Select S1,1 only and choose Additional marks in the Marker style frame:
Again, confirm the setting by pressing OK. The S-parameter plot of S1,1 should then look as follows:
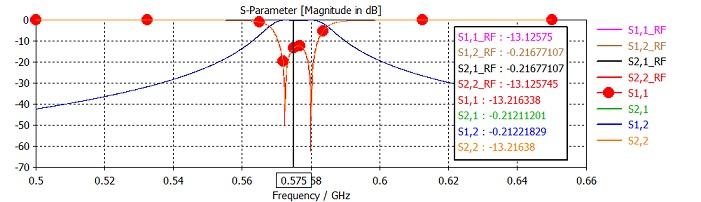
In the S-parameter plot, the axis
marker at the desired frequency is plotted and the corresponding S-parameter
values are given in a box. Next, select
1D Plot:
Markers
![]() Axis
Marker
Axis
Marker
![]() Calculate Field at Marker
Calculate Field at Marker
![]() or by pressing the right mouse button and selecting the Calculate field at axis marker option from the context menu.
or by pressing the right mouse button and selecting the Calculate field at axis marker option from the context menu.
Note that no additional equation sytem is solved because the solution was stored on disc for the adaptive mesh refinement frequency at 0.575 GHz. If the frequency were not calculated already, an additional frequency sample mark would appear at this frequency after one more equation system solve.
When the evaluation of the fields is finished, a dialog appears that asks if you would like to see the calculated fields.
Please click Yes. The main view will automatically show the E-field.
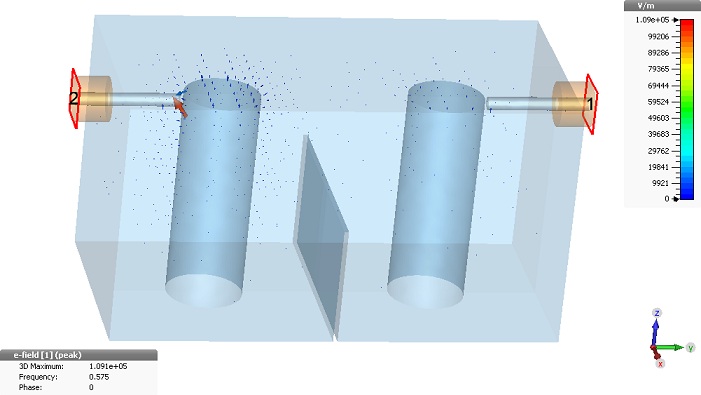
The result data will then be visualized in a three dimensional vector plot as shown in the above picture. Please refer to the Workflow and Solver Overview manual for more information on how to adjust the plot options.
In many cases, it is more important to visualize the fields
in a cross-section of the device. Therefore, please switch to the
2D field visualization mode by pressing the
2D/3D Plot:
Sectional View ![]() 3D Fields on 2D Plane
3D Fields on 2D Plane ![]() .
The field data should then be displayed as in the picture below. Please refer to the Workflow and Solver Overview manual or press the F1 key for
online help to obtain more information on field visualization options.
.
The field data should then be displayed as in the picture below. Please refer to the Workflow and Solver Overview manual or press the F1 key for
online help to obtain more information on field visualization options.
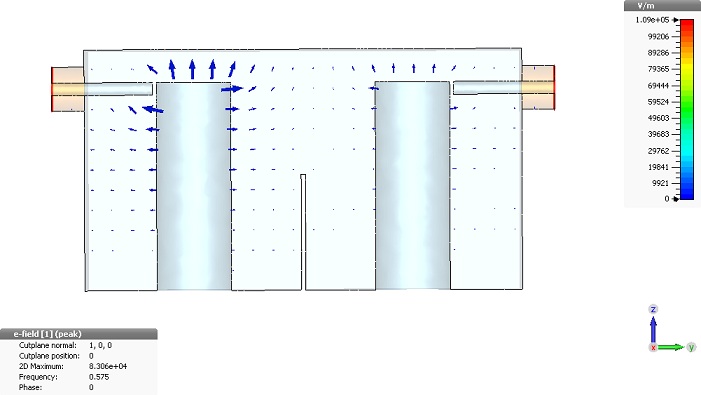
In addition to the graphical field visualization, some information text containing maximum field strength values and so on is also shown in the main window.
For S-parameter calculations with the frequency domain solver
tool please open the frequency domain solver control dialog box by pressing
Home:
Simulation ![]() Start Simulation
Start Simulation
![]() .
.
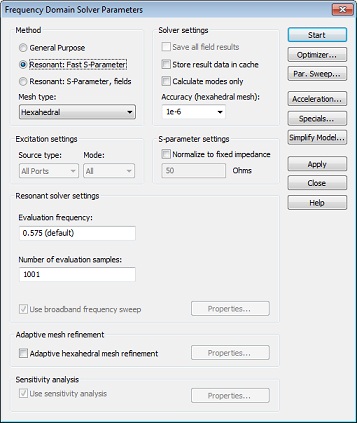
Click on the Resonant: Fast S-Parameter button that enables the corresponding solver, and change the mesh type to Hexahedral. For a first run disable the Adaptive hexahedral mesh refinement option.
Please check your settings in the dialog box before pressing the Start button.
Lets review the results.
o 1D Results (S-Parameters)
The S-Parameter can be plotted by clicking on the 1D Results
![]() S-Parameter
folder.
S-Parameter
folder.
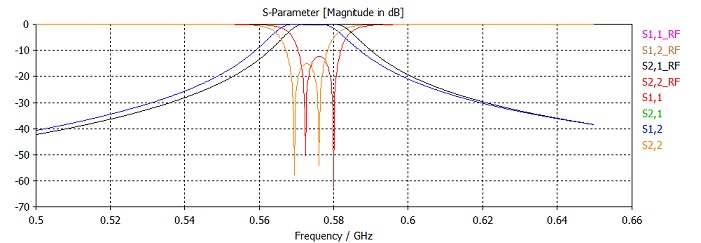
As expected, the bandwidth of the transmission S2,1 is quite small. The results without adaptive mesh refinement do not agree well with those obtained by the general purpose solver with fast resonant sweep and tetrahedral mesh, as indicated by S1,1_RF, S2,1_RF and so on.
o Accuracy Considerations
In
the example above, you have used the default initial mesh that has been automatically
generated by an expert system. The easiest way to prove the accuracy
of the results is to use the fully automatic mesh adaptation that can
be switched on by checking the Adaptive hexahedral mesh refinement
option in the solver control dialog box, Home:
Simulation ![]() Start Simulation
Start Simulation
![]() :
:
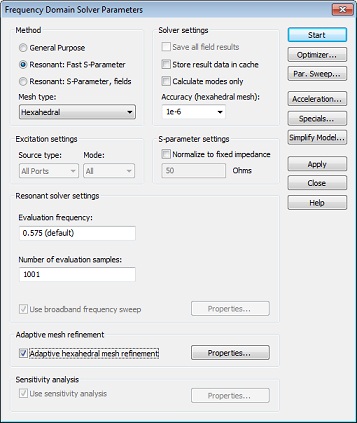
After activating the Adaptive hexahedral mesh refinement tool, you should now start the solver again by pressing the Start button. After a couple of minutes (during which the solver is running through mesh adaptation passes), the following dialog box will appear:
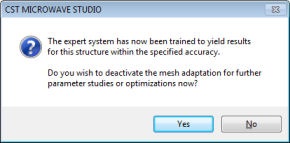
This dialog box notifies you that the desired accuracy limit of the S-parameters (2% by default) could be met by the adaptive mesh refinement. Because the expert systems settings have now been adjusted to achieve this level of accuracy, you may switch off the adaptation procedure for subsequent calculations (e.g. parameter sweeps or optimizations).
After
the mesh adaptation procedure is complete, you can visualize the maximum
relative difference of the S-parameters for two subsequent passes by selecting
1D Results ![]() Adaptive Meshing
Adaptive Meshing ![]() Delta S from the navigation tree:
Delta S from the navigation tree:
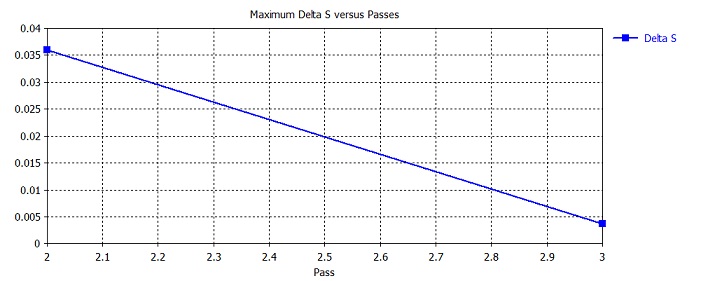
As
evident from the above figure, the automatic mesh adaptation procedure
requires three passes to achieve convergence for this challenging filter
structure. This indicates that it is necessary to run the mesh adaptation
or perform a manual mesh refinement to achieve highly accurate results.
When examining the progression of the transmission S2,1 during the adaptive
mesh refinement (1D Results ![]() Adaptive Meshing
Adaptive Meshing ![]() S-Parameters
S-Parameters ![]() S2,1), you can observe that the pass band has moved towards
higher frequencies in the course of the adaptive mesh refinement:
S2,1), you can observe that the pass band has moved towards
higher frequencies in the course of the adaptive mesh refinement:

Finally, the most interesting results are the S-parameters as shown below:
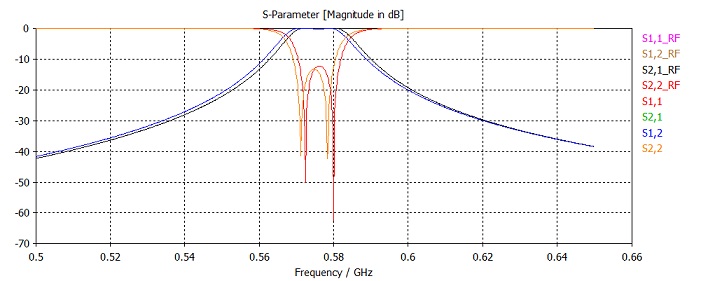
The final S-parameters differ from the first results obtained with the initial mesh created by the expert system, and are closer to the results of the fast resonant sweep with tetrahedral mesh. The trend observed above, namely that the pass band moves towards higher frequencies with hexahedral mesh refinement, will continue if the adaptive hexahedral mesh refinement is continued. In general, accurate S-parameter results for filter structures can only be obtained by mesh convergence studies. These studies can be carried out either by manually changing the settings of the expert system or, as demonstrated here, by running the automatic mesh adaptation tool.
The advantage of this expert system based mesh refinement procedure over traditional adaptive schemes is that the mesh adaptation must be carried out only once for each device to determine the optimum settings for the expert system. Afterwards, there is no need for time-consuming mesh adaptation cycles during parameter sweeps or optimizations.
Congratulations! You have just completed the filter tutorial that should have provided you with a good working knowledge on how to use the Frequency Domain solvers to calculate S-parameters of filter structures. The following topics have been covered:
1. General modeling considerations, using templates, etc.
2. Define basic structure elements such as bricks and cylinders.
3. Use the working coordinate system to simplify the shape creation.
4. Create copies of existing shapes by using transformations.
5. Define the frequency range, boundary conditions and symmetries.
6. Run the Frequency Domain solvers and display S-parameters together with their sensitivities, and field patterns.
7. Obtain accurate and converged results using the automatic mesh adaptation.
You can obtain more information for each particular step from the online help system that can be activated by pressing either the Help button in each dialog box or the F1 key at any time to obtain context sensitive information.
In some cases we have referred to the Workflow and Solver Overview manual, which is also a good source of information for general topics.
In addition to this tutorial, you can find additional Frequency Domain Solver examples in the examples folder in your installation directory. Each of these examples contains a Readme item in the navigation tree that will give you some more information about the particular device.
You should also consider using the transient solver to calculate the S-parameters for filter structures. Please check out the other tutorials and the transient solver examples in the examples folder for more information.
Finally, you should refer to the Online documentation for more in-depth information on issues such as the fundamental principles of the simulation method, mesh generation, usage of macros to automate common tasks, etc.
And last but not least: Please visit one of the training classes that are regularly held at a location near you. Thank you for using CST MICROWAVE STUDIO!
HFSS视频教程 ADS视频教程 CST视频教程 Ansoft Designer 中文教程
|
Copyright © 2006 - 2013 微波EDA网, All Rights Reserved 业务联系:mweda@163.com |
|